第11章 数値
JavaScriptはすべての数値に対して単一型を使用します。すべての数値を浮動小数点数として扱います。ただし、小数点以下の桁がない場合は小数点は表示されません。
> 5.000 5
内部的には、ほとんどのJavaScriptエンジンは最適化を行い、浮動小数点数と整数を区別します(詳細:JavaScriptにおける整数)。しかし、これはプログラマには見えないことです。
JavaScriptの数値は、IEEE浮動小数点演算標準(IEEE 754)に基づくdouble(64ビット)値です。この標準は多くのプログラミング言語で使用されています。
数値リテラル
数値リテラルは整数、浮動小数点数、または(整数)16進数にすることができます。
> 35 // integer 35 > 3.141 // floating point 3.141 > 0xFF // hexadecimal 255
リテラルへのメソッドの呼び出し
数値リテラルでは、プロパティにアクセスするためのドットを、小数点と区別する必要があります。数値リテラル123でtoString()を呼び出したい場合、次のオプションがあります。
123..toString()123.toString()// space before the dot123.0.toString()(123).toString()
数値への変換
| 値 | 結果 |
|
|
|
|
ブール値 |
|
| |
数値 | 入力と同じ(変換なし) |
文字列 | 文字列内の数値を解析します(先頭と末尾の空白を無視します)。空文字列は0に変換されます。例: |
オブジェクト |
|
空文字列を数値に変換する場合、NaNの方が適切な結果と言えるでしょう。結果は、1990年代半ばの他のプログラミング言語と同様に、空の数値入力フィールドに対応するために0が選択されました。[14]
数値への手動変換
任意の値を数値に変換する最も一般的な2つの方法は次のとおりです。
| (コンストラクタとしてではなく、関数として呼び出されます) |
|
より記述的なので、Number()を好みます。いくつかの例を以下に示します。
> Number('')
0
> Number('123')
123
> Number('\t\v\r12.34\n ') // ignores leading and trailing whitespace
12.34
> Number(false)
0
> Number(true)
1parseFloat()
グローバル関数parseFloat()は、値を数値に変換する別の方法を提供します。しかし、後ほど説明するように、通常はNumber()の方が適切な選択です。このコード:
parseFloat(str)
strを文字列に変換し、先頭の空白を取り除き、浮動小数点数である最長のプレフィックスを解析します。そのようなプレフィックスが存在しない場合(例:空文字列)、NaNが返されます。
parseFloat()とNumber()の比較
parseFloat()を非文字列に適用すると、解析する前に引数を文字列に強制変換するため、効率が低下します。その結果、Number()が実際の数値に変換する多くの値が、parseFloat()によってNaNに変換されます。> parseFloat(true) // same as parseFloat('true') NaN > Number(true) 1 > parseFloat(null) // same as parseFloat('null') NaN > Number(null) 0parseFloat()は空文字列をNaNとして解析します。> parseFloat('') NaN > Number('') 0parseFloat()は最後の有効な文字まで解析するため、望ましくない結果が得られる可能性があります。> parseFloat('123.45#') 123.45 > Number('123.45#') NaNparseFloat()は先頭の空白を無視し、無効な文字(空白を含む)の前に停止します。> parseFloat('\t\v\r12.34\n ') 12.34Number()は先頭と末尾の両方の空白を無視しますが(ただし、他の無効な文字はNaNになります)。
特殊な数値
JavaScriptにはいくつかの特殊な数値があります。
- 2つのエラー値、
NaNとInfinity。 - 2つのゼロ値、
+0と-0。JavaScriptには、正のゼロと負のゼロの2つのゼロがあります。これは、数値の符号と大きさが別々に格納されているためです。本書の大部分では、単一のゼロがあると想定しており、JavaScriptで2つのゼロがあることはほとんど見られません。
NaN
エラー値NaN(「数値ではない」の略)は、皮肉にも数値です。
> typeof NaN 'number'
これは、次のようなエラーによって生成されます。
数値を解析できませんでした。
> Number('xyz') NaN > Number(undefined) NaN演算が失敗しました。
> Math.acos(2) NaN > Math.log(-1) NaN > Math.sqrt(-1) NaN
オペランドのいずれかが
NaNです(これにより、長い計算中にエラーが発生した場合、最終結果でそれを確認できます)。> NaN + 3 NaN > 25 / NaN NaN
落とし穴:値がNaNかどうかを確認する
NaNは、自分自身と等しくない唯一の値です。
> NaN === NaN false
厳密等価演算子(===)はArray.prototype.indexOfでも使用されます。そのため、そのメソッドを使用して配列内でNaNを検索することはできません。
> [ NaN ].indexOf(NaN) -1
値がNaNかどうかを確認する場合は、グローバル関数isNaN()を使用する必要があります。
> isNaN(NaN) true > isNaN(33) false
しかし、isNaNは、最初にそれらを数値に変換するため、数値以外の値では正しく機能しません。この変換によってNaNが生成され、関数が誤ってtrueを返す可能性があります。
> isNaN('xyz')
trueしたがって、isNaNを型チェックと組み合わせるのが最善です。
functionmyIsNaN(value){returntypeofvalue==='number'&&isNaN(value);}
あるいは、値が自分自身と等しくないかどうかを確認することもできます(NaNはこの特性を持つ唯一の値です)。しかし、これはあまり分かりやすいものではありません。
functionmyIsNaN(value){returnvalue!==value;}
この動作はIEEE 754によって規定されていることに注意してください。「比較述語の詳細」のセクション7.11で述べられているように:[15]
すべてのNaNは、自分自身を含むすべてと順序なしに比較されます。
Infinity
Infinityは、2つの問題のいずれかを示すエラー値です。数値の大きさが大きすぎて表現できないか、ゼロ除算が発生しました。
Infinityは他のどの数値(NaNを除く)よりも大きいです。同様に、-Infinityは他のどの数値(NaNを除く)よりも小さいです。そのため、最小値または最大値を探す場合など、デフォルト値として役立ちます。
エラー:数値の大きさが大きすぎる
数値の大きさがどの程度大きくなれるかは、内部表現(数値の内部表現で説明)によって決まり、これは次の算術積です。
- 仮数(2進数1.f1f2...)
- 指数乗の2
指数は−1023と1024の間(ただし除く)でなければなりません。指数が小さすぎると、数値は0になります。指数が大きすぎると、Infinityになります。21023はまだ表現できますが、21024は表現できません。
> Math.pow(2, 1023) 8.98846567431158e+307 > Math.pow(2, 1024) Infinity
Infinityを使用した計算
Infinityを別のInfinityで「中和」しようとすると、エラー結果NaNが得られます。
> Infinity - Infinity NaN > Infinity / Infinity NaN
Infinityを超えようとすると、依然としてInfinityが得られます。
> Infinity + Infinity Infinity > Infinity * Infinity Infinity
Infinityの確認
厳密等価と緩い等価はInfinityで正常に機能します。
> var x = Infinity; > x === Infinity true
さらに、グローバル関数isFinite()を使用すると、値が実際の数値(無限でもNaNでもない)かどうかを確認できます。
> isFinite(5) true > isFinite(Infinity) false > isFinite(NaN) false
2つのゼロ
JavaScriptの数値は大きさと符号を別々に保持するため、非負の数には負の数も含まれ、0も同様です。
その理由は、数値をデジタルで表現するたびに、エンコードの精度が不足しているため、0との区別がつかないほど小さくなる可能性があるためです。符号付きゼロを使用すると、「どの方向から」ゼロに近づいたかを記録できます。つまり、ゼロと見なされる前の数値の符号を記録できます。Wikipediaは符号付きゼロの長所と短所をうまくまとめています。
IEEE 754に符号付きゼロを含めることで、特に複雑な初等関数を使用する計算において、数値精度を大幅に向上させることが可能であると主張されています。一方、符号付きゼロの概念は、負のゼロはゼロと同じであるという、ほとんどの数学分野(およびほとんどの数学コース)で行われている一般的な仮定に反しています。負のゼロを許容する表現は、プログラムのエラーの原因となる可能性があります。ソフトウェア開発者は、2つのゼロ表現が数値比較では等しく動作するにもかかわらず、異なるビットパターンであり、一部の演算では異なる結果を生成するということに気づいていない(または忘れてしまう)可能性があるためです。
ベストプラクティス:単一のゼロがあると想定する
JavaScriptは、2つのゼロがあるという事実を隠すために非常に努力しています。通常は違いが問題にならないことを考えると、単一のゼロという幻想に沿ってプレイすることをお勧めします。この幻想がどのように維持されているかを調べてみましょう。
JavaScriptでは、通常0と書きますが、これは+0を意味します。しかし、-0も単に0として表示されます。これは、ブラウザのコマンドラインまたはNode.jsのREPLを使用するときに表示されるものです。
> -0 0
これは、標準のtoString()メソッドが両方のゼロを同じ'0'に変換するためです。
> (-0).toString() '0' > (+0).toString() '0'
> +0 === -0 true
Array.prototype.indexOfは要素の検索に===を使用し、幻想を維持します。
> [ -0, +0 ].indexOf(+0) 0 > [ +0, -0 ].indexOf(-0) 0
順序演算子もゼロを等しいと見なします。
> -0 < +0 false > +0 < -0 false
2つのゼロを区別する
2つのゼロが実際に異なることをどのように確認できますか?ゼロで除算できます(-Infinityと+Infinityは===で区別できます)。
> 3 / -0 -Infinity > 3 / +0 Infinity
ゼロ除算を実行する別の方法はMath.pow()を使用することです(数値関数を参照)。
> Math.pow(-0, -1) -Infinity > Math.pow(+0, -1) Infinity
Math.atan2()(三角関数を参照)もゼロが異なることを明らかにします。
> Math.atan2(-0, -1) -3.141592653589793 > Math.atan2(+0, -1) 3.141592653589793
2つのゼロを区別する標準的な方法は、ゼロ除算です。したがって、負のゼロを検出するための関数は、次のようになります。
functionisNegativeZero(x){returnx===0&&(1/x<0);}
これが関数の実行例です。
> isNegativeZero(0) false > isNegativeZero(-0) true > isNegativeZero(33) false
数値の内部表現
JavaScriptの数値は64ビットの精度を持ち、これは倍精度(一部のプログラミング言語ではdouble型)とも呼ばれます。内部表現はIEEE 754規格に基づいています。64ビットは、数値の符号、指数、および仮数に次のように分配されます
| 符号 | 指数 ∈ [−1023, 1024] | 仮数 |
1ビット | 11ビット | 52ビット |
ビット63 | ビット62~52 | ビット51~0 |
数値の値は、次の式で計算されます
(–1)符号 × %1.仮数 × 2指数
先頭に付いたパーセント記号(%)は、中央の数値が2進表記であることを意味します。1に続いて、2進小数点、そして2進仮数(自然数)の2進桁が続きます。この表現の例をいくつか示します。
+0 | (符号 = 0、仮数 = 0、指数 = −1023) | |
–0 | (符号 = 1、仮数 = 0、指数 = −1023) | |
1 | = (−1)0 × %1.0 × 20 | (符号 = 0、仮数 = 0、指数 = 0) |
2 | = (−1)0 × %1.0 × 21 | |
3 | = (−1)0 × %1.1 × 21 | (符号 = 0、仮数 = 251、指数 = 0) |
0.5 | = (−1)0 × %1.0 × 2−1 | |
–1 | = (−1)1 × %1.0 × 20 |
+0、−0、および3のエンコーディングは、次のように説明できます。
- ±0:仮数は常に1を先頭に付けるため、これを用いて0を表すことはできません。したがって、JavaScriptでは、仮数0と特別な指数−1023を使用してゼロをエンコードします。符号は正または負のいずれかになるため、JavaScriptには2つのゼロがあります(Two Zerosを参照)。
- 3:ビット51は、仮数の最上位ビットです。そのビットは1です。
特別な指数
前述の数値の表現は正規化されています。その場合、指数eは−1023 < e < 1024の範囲にあります(下限と上限は除く)。−1023と1024は特別な指数です。
- 1024は、
NaNやInfinityなどのエラー値に使用されます。 –1023は、次のように使用されます。
- ゼロ(仮数が0の場合、既に説明したとおり)
- ゼロに近い小さな数(仮数が0でない場合)
両方の用途を可能にするために、異なる、非正規化と呼ばれる表現が使用されます。
(–1)符号 × %0.仮数 × 2–1022
比較すると、正規化された表現における最小の数値(ゼロに最も近い)は次のとおりです。
(–1)符号 × %1.仮数 × 2–1022
非正規化された数値の方が小さいのは、先頭の桁が1ではないためです。
丸め誤差の処理
JavaScriptの数値は通常、10進浮動小数点数として入力されますが、内部的には2進浮動小数点数として表現されます。そのため、不正確さが生じます。その理由を理解するために、JavaScriptの内部記憶形式を忘れて、10進浮動小数点数と2進浮動小数点数で正確に表現できる分数を一般的に見てみましょう。10進数システムでは、すべての分数は、仮数mを10の累乗で割ったものです。
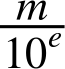
そのため、分母には10しかありません。![]() を10進浮動小数点数として正確に表現することはできません。分母に3を入れる方法がないからです。2進浮動小数点数は、分母に2しかありません。どの10進浮動小数点数を2進数としてうまく表現できるか、できないかを調べてみましょう。分母に2しかない場合、10進数は表現できます。
を10進浮動小数点数として正確に表現することはできません。分母に3を入れる方法がないからです。2進浮動小数点数は、分母に2しかありません。どの10進浮動小数点数を2進数としてうまく表現できるか、できないかを調べてみましょう。分母に2しかない場合、10進数は表現できます。
- 0.5dec =
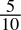 =
= 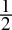 = 0.1bin
= 0.1bin - 0.75dec =
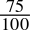 =
= 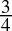 = 0.11bin
= 0.11bin - 0.125dec =
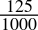 =
= 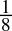 = 0.001bin
= 0.001bin
他の分数は、(素因数分解後)分母に2以外の数があるため、正確に表現できません。
- 0.1dec =
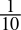 =
= 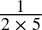
- 0.2dec =
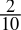 =
= 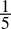
JavaScriptが内部的に0.1を正確に格納していないことは、通常は見えません。しかし、10の十分に高い累乗をかけることで、それを可視化することができます。
> 0.1 * Math.pow(10, 24) 1.0000000000000001e+23
そして、2つの不正確に表現された数値を加算すると、その結果が不正確すぎて、不正確さが目に見えるようになることがあります。
> 0.1 + 0.2 0.30000000000000004
別の例
> 0.1 + 1 - 1 0.10000000000000009
丸め誤差により、ベストプラクティスとして、非整数を直接比較することは避けるべきです。代わりに、丸め誤差の上限を考慮する必要があります。このような上限は、マシンイプシロンと呼ばれます。倍精度のための標準的なイプシロン値は2−53です。
varEPSILON=Math.pow(2,-53);functionepsEqu(x,y){returnMath.abs(x-y)<EPSILON;}
epsEqu()は、通常の比較では不十分な場合に正しい結果を保証します。
> 0.1 + 0.2 === 0.3 false > epsEqu(0.1+0.2, 0.3) true
JavaScriptにおける整数
前述のように、JavaScriptには浮動小数点数しかありません。整数は内部的に2つの方法で現れます。まず、ほとんどのJavaScriptエンジンは、小数点以下の桁のない十分に小さい数値を整数として(例えば31ビットで)格納し、可能な限りその表現を維持します。数値の大きさが大きくなりすぎたり、小数点以下の桁が現れたりすると、浮動小数点表現に戻す必要があります。
第二に、ECMAScript仕様には整数演算子があります。つまり、すべてのビット演算子です。これらの演算子は、オペランドを32ビット整数に変換し、32ビット整数を返します。仕様では、整数は数値に小数点以下の桁がないことを意味し、32ビットは特定の範囲内にあることを意味します。エンジンにとって、32ビット整数は、実際の整数(浮動小数点ではない)表現を通常導入または維持できることを意味します。
整数の範囲
内部的には、次の整数の範囲がJavaScriptで重要です。
安全な整数(Safe Integersを参照)、JavaScriptがサポートする、実際的に使用可能な最大の整数の範囲
- 53ビットと符号、範囲(−253、253)
配列インデックス(Array Indicesを参照)
- 32ビット、符号なし
- 最大長:232−1
- インデックスの範囲:[0、232−1)(最大長を除く!)
ビット演算オペランド(Bitwise Operatorsを参照)
- 符号なし右シフト演算子(
>>>):32ビット、符号なし、範囲[0、232) - その他のすべてのビット演算子:32ビット、符号を含む、範囲[−231、231)
- 符号なし右シフト演算子(
「文字コード」、数値としてのUTF-16コードユニット
String.fromCharCode()で受け入れられる(String Constructor Methodを参照)String.prototype.charCodeAt()で返される(Extract Substringsを参照)- 16ビット、符号なし
浮動小数点数としての整数の表現
JavaScriptは最大53ビットの大きさの整数値しか処理できません(仮数の52ビットと1つの間接ビット、指数による;詳細はThe Internal Representation of Numbersを参照)。
次の表は、JavaScriptが53ビットの整数を浮動小数点数としてどのように表現するかを示しています。
| ビット | 範囲 | エンコーディング |
1ビット | 0 | |
1ビット | 1 | %1 × 20 |
2ビット | 2~3 | %1.f51 × 21 |
3ビット | 4~7 = 22~(23−1) | %1.f51f50 × 22 |
4ビット | 23~(24−1) | %1.f51f50f49 × 23 |
⋯ | ⋯ | ⋯ |
53ビット | 252~(253−1) | %1.f51⋯f0 × 252 |
整数を表すビットの固定されたシーケンスはありません。代わりに、仮数%1.fは指数によってシフトされ、先頭の桁1が正しい位置に配置されます。ある意味、指数は実際に使用されている仮数の桁数をカウントします(残りの桁は0です)。つまり、2ビットの場合は仮数の1桁を使用し、53ビットの場合は仮数のすべての桁を使用します。さらに、253は%1.0 × 253として表現できますが、より大きな数値では問題が発生します。
| ビット | 範囲 | エンコーディング |
54ビット | 253~(254−1) | %1.f51⋯f00 × 253 |
55ビット | 254~(255−1) | %1.f51⋯f000 × 254 |
⋯ |
54ビットの場合、最下位桁は常に0であり、55ビットの場合、最下位2桁は常に0になります。つまり、54ビットの場合、2つに1つの数値しか表現できず、55ビットの場合には4つに1つの数値しか表現できません。
> Math.pow(2, 53) - 1 // OK 9007199254740991 > Math.pow(2, 53) // OK 9007199254740992 > Math.pow(2, 53) + 1 // can't be represented 9007199254740992 > Math.pow(2, 53) + 2 // OK 9007199254740994
安全な整数
JavaScriptは、範囲 −253 < i < 253 内の整数iのみを安全に表現できます。このセクションでは、それが何を意味し、どのような結果になるかを調べます。これは、Mark S. Millerによるes-discussメーリングリストへのメールに基づいています。
安全な整数の概念は、JavaScriptで数学的整数がどのように表現されるかに関係しています。範囲(−253, 253)(下限と上限を除く)では、JavaScriptの整数は安全です。数学的整数とそのJavaScriptでの表現との間に一対一の対応関係があります。
この範囲を超えると、JavaScriptの整数は安全ではないです。2つ以上の数学的整数が同じJavaScript整数として表現されます。たとえば、253から始めると、JavaScriptは2つに1つの数学的整数しか表現できません(前のセクションでその理由を説明しています)。したがって、安全なJavaScript整数とは、単一の数学的整数を明確に表す整数です。
ECMAScript 6での定義
ECMAScript 6では、次の定数が提供されます。
Number.MAX_SAFE_INTEGER=Math.pow(2,53)-1;Number.MIN_SAFE_INTEGER=-Number.MAX_SAFE_INTEGER;
また、整数が安全かどうかを判断する関数も提供されます。
Number.isSafeInteger=function(n){return(typeofn==='number'&&Math.round(n)===n&&Number.MIN_SAFE_INTEGER<=n&&n<=Number.MAX_SAFE_INTEGER);}
与えられた値nに対して、この関数はまずnが数値であり整数であるかどうかをチェックします。両方のチェックに成功した場合、nはMIN_SAFE_INTEGER以上であり、MAX_SAFE_INTEGER以下であれば安全です。
算術演算の安全な結果
算術演算の結果が正しいことをどのようにして確認できますか?たとえば、次の結果は明らかに正しくありません。
> 9007199254740990 + 3 9007199254740992
2つの安全なオペランドがありますが、結果は安全ではありません。
> Number.isSafeInteger(9007199254740990) true > Number.isSafeInteger(3) true > Number.isSafeInteger(9007199254740992) false
次の結果も正しくありません。
> 9007199254740995 - 10 9007199254740986
今回は結果は安全ですが、オペランドの1つは安全ではありません。
> Number.isSafeInteger(9007199254740995) false > Number.isSafeInteger(10) true > Number.isSafeInteger(9007199254740986) true
したがって、整数演算子opを適用した結果は、すべてのオペランドと結果が安全な場合にのみ正しいことが保証されます。より正式には
isSafeInteger(a) && isSafeInteger(b) && isSafeInteger(a op b)
a op bが正しい結果であることを意味します。
整数への変換
JavaScriptでは、すべての数値は浮動小数点数です。整数は小数点以下の部分のない浮動小数点数です。数値nを整数に変換するということは、「最も近い」整数を見つけることを意味します(「最も近い」の意味は、変換方法によって異なります)。この変換を実行するには、いくつかの方法があります。
Math関数Math.floor()、Math.ceil()、およびMath.round()(Math.floor()、Math.ceil()、およびMath.round()による整数を参照)- カスタム関数
ToInteger()(カスタム関数ToInteger()による整数を参照) - バイナリビット演算子(ビット演算子による32ビット整数を参照)
- グローバル関数
parseInt()(parseInt()による整数を参照)
ネタバレ:1番目が通常最適な選択肢であり、2番目と3番目はニッチな用途があり、4番目は文字列の解析には問題ありませんが、数値を整数に変換するためには適していません。
Math.floor()、Math.ceil()、およびMath.round()による整数
次の3つの関数は、数値を整数に変換する通常最適な方法です。
Math.floor()は、引数を最も近い小さい整数に変換します:> Math.floor(3.8) 3 > Math.floor(-3.8) -4
Math.ceil()は、引数を最も近い大きい整数に変換します:> Math.ceil(3.2) 4 > Math.ceil(-3.2) -3
Math.round()は、引数を最も近い整数に変換します:> Math.round(3.2) 3 > Math.round(3.5) 4 > Math.round(3.8) 4
-3.5を丸めた結果は驚くかもしれません。> Math.round(-3.2) -3 > Math.round(-3.5) -3 > Math.round(-3.8) -4
したがって、
Math.round(x)は次のと同じです。Math.floor(x+0.5)
カスタム関数ToInteger()による整数
任意の値を整数に変換するためのもう1つの良い方法は、内部ECMAScript演算ToInteger()です。これは、浮動小数点数の小数部分を削除します。JavaScriptで使用可能であれば、次のように動作します。
> ToInteger(3.2) 3 > ToInteger(3.5) 3 > ToInteger(3.8) 3 > ToInteger(-3.2) -3 > ToInteger(-3.5) -3 > ToInteger(-3.8) -3
ECMAScript仕様では、ToInteger(number)の結果を次のように定義しています。
sign(number) × floor(abs(number))
その機能のために、この式は比較的複雑です。なぜならfloorは最も近い大きい整数を探し求めるため、負の整数の小数部分を削除したい場合は、最も近い小さい整数を探し求める必要があるからです。次のコードは、JavaScriptでこの演算を実装します。sign演算を避けるために、数値が負の場合はceilを使用します。
functionToInteger(x){x=Number(x);returnx<0?Math.ceil(x):Math.floor(x);}
バイナリビット演算子(バイナリビット演算子を参照)は、オペランドの少なくとも1つを32ビット整数に変換し、32ビット整数でもある結果を生成します。したがって、もう一方のオペランドを適切に選択すれば、任意の数値を(符号付きまたは符号なし)32ビット整数に高速に変換する方法が得られます。
ビットごとのOR(|)
マスク(第2オペランド)が0の場合、ビットは変更されず、結果は第1オペランド(符号付き32ビット整数に強制変換されたもの)になります。これは、この種の強制変換を実行する標準的な方法であり、たとえばasm.jsによって使用されます(JavaScriptは十分に高速ですか?を参照)。
// Convert x to a signed 32-bit integerfunctionToInt32(x){returnx|0;}
ToInt32()は小数部分を削除し、232を法とする剰余を適用します。
> ToInt32(1.001) 1 > ToInt32(1.999) 1 > ToInt32(1) 1 > ToInt32(-1) -1 > ToInt32(Math.pow(2, 32)+1) 1 > ToInt32(Math.pow(2, 32)-1) -1
シフト演算子
ビットごとのORで機能したのと同じトリックがシフト演算子でも機能します。0ビットだけシフトすると、シフト演算の結果は、第1オペランド(32ビット整数に強制変換されたもの)になります。ECMAScript仕様の演算をシフト演算子で実装する例をいくつか示します。
// Convert x to a signed 32-bit integerfunctionToInt32(x){returnx<<0;}// Convert x to a signed 32-bit integerfunctionToInt32(x){returnx>>0;}// Convert x to an unsigned 32-bit integerfunctionToUint32(x){returnx>>>0;}
> ToUint32(-1) 4294967295 > ToUint32(Math.pow(2, 32)-1) 4294967295 > ToUint32(Math.pow(2, 32)) 0
ビット演算子を使用して整数への強制変換を行うべきですか?
わずかな効率の向上に見合うだけの価値があるかどうかは、自分で判断する必要があります。また、ビット演算子は人工的に32ビットに制限されていることに注意してください。これは、多くの場合、必要でも便利でもありません。Math関数の1つを、場合によってはMath.abs()に追加して使用すると、より分かりやすく、より良い選択肢と言えるでしょう。
parseInt()による整数
parseInt() 関数:
parseInt(str,radix?)
文字列str(非文字列は強制変換されます)を整数として解析します。この関数は先頭の空白を無視し、見つかる限り連続する有効な数字を考慮します。
基数
基数の範囲は2 ≤ radix ≤ 36です。これは、解析する数値の基数を決定します。基数が10より大きい場合、0~9に加えて、文字が数字として使用されます(大文字と小文字は区別されません)。
radixが省略されている場合、strが「0x」または「0X」で始まる場合を除き、10と見なされます。その場合、radixは16(16進数)に設定されます。
> parseInt('0xA')
10radixが既に16の場合、16進数のプレフィックスは省略可能です。
> parseInt('0xA', 16)
10
> parseInt('A', 16)
10これまでのところ、ECMAScript仕様に従ったparseInt()の動作について説明しました。さらに、一部のエンジンでは、strがゼロで始まる場合、基数を8に設定します。
> parseInt('010')
8
> parseInt('0109') // ignores digits ≥ 8
8したがって、基数を常に明示的に指定し、常に2つの引数でparseInt()を呼び出すのが最善です。
いくつかの例を以下に示します。
> parseInt('')
NaN
> parseInt('zz', 36)
1295
> parseInt(' 81', 10)
81
> parseInt('12**', 10)
12
> parseInt('12.34', 10)
12
> parseInt(12.34, 10)
12数値を整数に変換するためにparseInt()を使用しないでください。最後の例は、数値を整数に変換するためにparseInt()を使用できるかもしれないという希望を与えてくれます。しかしながら、変換が正しくない例を以下に示します。
> parseInt(1000000000000000000000.5, 10) 1
説明
引数は最初に文字列に変換されます。
> String(1000000000000000000000.5) '1e+21'
parseIntは「e」を整数桁とは見なさないため、1の後に解析を停止します。別の例を以下に示します。
> parseInt(0.0000008, 10) 8 > String(0.0000008) '8e-7'
概要
parseInt()は、数値を整数に変換するために使用すべきではありません。文字列への強制変換は不要な迂回であり、それでも結果は常に正しいとは限りません。
parseInt()は文字列の解析には役立ちますが、最初の無効な数字で停止することに注意する必要があります。Number()(関数Numberを参照)による文字列の解析はそれほど寛容ではありませんが、非整数になる可能性があります。
算術演算子
次の演算子は数値で使用できます。
-
number1 + number2 数値の加算。ただし、オペランドのいずれかが文字列の場合を除きます。その場合、両方のオペランドは文字列に変換され、連結されます(プラス演算子(+)を参照)。
> 3.1 + 4.3 7.4 > 4 + ' messages' '4 messages'
-
number1 - number2 - 減算。
-
number1 * number2 - 乗算。
-
number1 / number2 - 除算。
-
number1 % number2 剰余
> 9 % 7 2 > -9 % 7 -2
警告
この演算は剰余ではありません。第1オペランドと同じ符号の値を返します(詳細は後述)。
-
-number - オペランドを反転します。
-
+number - オペランドをそのまま残します。非数値は数値に変換されます。
-
++variable、--variable 1だけ増分(または減分)した後の変数の現在の値を返します:
> var x = 3; > ++x 4 > x 4
-
variable++、variable-- 変数の値を1だけ増分(または減分)し、それを返します。
> var x = 3; > x++ 3 > x 4
ニーモニック:増分(++)と減分(--)演算子
オペランドの位置は、増分(または減分)する前または後にそれが返されるかどうかを覚えるのに役立ちます。オペランドが増分演算子の前にある場合、増分する前に返されます。オペランドが演算子の後にある場合、増分してから返されます。(減分演算子も同様に機能します)。
ビット演算子
JavaScriptには、32ビット整数で動作するいくつかのビット演算子があります。つまり、オペランドを32ビット整数に変換し、32ビット整数である結果を生成します。これらの演算子のユースケースには、バイナリプロトコルの処理、特殊なアルゴリズムなどがあります。
背景知識
このセクションでは、ビット演算子の理解に役立ついくつかの概念について説明します。
2進補数
2進数の2進補数(または逆数)を計算する一般的な2つの方法は次のとおりです。
- 1の補数
数値
xの1の補数~xは、32桁の各桁を反転することで計算されます。4桁の数値を用いて1の補数を説明しましょう。1100の1の補数は0011です。ある数とその1の補数を足すと、すべての桁が1の数になります。1 + ~1 = 0001 + 1110 = 1111
- 2の補数
数値
xの2の補数-xは、1の補数に1を加えたものです。ある数とその2の補数を足すと0になります(最上位桁を超えるオーバーフローは無視します)。4桁の数値を用いた例を以下に示します。1 + -1 = 0001 + 1111 = 0000
符号付き32ビット整数
32ビット整数には明示的な符号がありませんが、負の数をエンコードすることは可能です。例えば、−1は1の2の補数としてエンコードできます。結果に1を加えると0になります(32ビット以内)。正の数と負の数の境界は流動的です。4294967295 (232−1)と−1はここで同じ整数です。しかし、そのような整数をJavaScriptの数値(明示的な符号を持つ)に変換する際、符号を決定する必要があります。そのため、符号付き32ビット整数は2つのグループに分けられます。
- 最上位ビットが0:数値は0または正。
- 最上位ビットが1:数値は負。
最上位ビットはしばしば符号ビットと呼ばれます。従って、符号付き32ビット整数として解釈された4294967295は、JavaScriptの数値に変換されると−1になります。
> ToInt32(4294967295) -1
ToInt32()については、ビット演算子による32ビット整数で説明しています。
注意
符号なし右シフト演算子(>>>)のみが符号なし32ビット整数で機能します。他のすべてのビット演算子は符号付き32ビット整数で機能します。
2進数の入力と出力
parseInt(str, 2)(parseInt()による整数を参照)は、2進表記(基数2)の文字列strを解析します。 例えば:> parseInt('110', 2) 6num.toString(2)(Number.prototype.toString(radix?)を参照)は、数値numを2進表記の文字列に変換します。 例えば:> 6..toString(2) '110'
ビット単位のNOT演算子
> (~parseInt('11111111111111111111111111111111', 2)).toString(2)
'0'2項ビット演算子
JavaScriptには3つの2項ビット演算子があります。
> (parseInt('11001010', 2) & parseInt('1111', 2)).toString(2) '1010'> (parseInt('11001010', 2) | parseInt('1111', 2)).toString(2) '11001111'number1 ^ number2(ビット単位のXOR;排他的OR)> (parseInt('11001010', 2) ^ parseInt('1111', 2)).toString(2) '11000101'
2進数のビット演算子を直感的に理解する方法は2つあります。
- ビットごとのブール演算
以下の式において、
niは数値nのiビット目をブール値として解釈したものです(0はfalse、1はtrue)。例えば、20はfalseです。21はtrueです。- AND:
resulti = number1i && number2i - OR:
resulti = number1i || number2i XOR:
resulti = number1i ^^ number2i演算子
^^は存在しません。もし存在すれば、このようになります(オペランドのちょうど1つがtrueの場合、結果はtrueになります)。x^^y===(x&&!y)||(!x&&y)
- AND:
number2を用いたnumber1のビット変更- AND:
number2で設定されているnumber1のビットのみを保持します。この演算はマスクとも呼ばれ、number2がマスクになります。 - OR:
number2で設定されているnumber1のすべてのビットを設定し、他のすべてのビットは変更しません。 - XOR:
number2で設定されているnumber1のすべてのビットを反転し、他のすべてのビットは変更しません。
- AND:
ビットシフト演算子
JavaScriptには3つのビットシフト演算子があります。
> (parseInt('1', 2) << 1).toString(2) '10'number >> digitCount(符号付き右シフト):32ビット2進数は符号付きとして解釈されます(前のセクションを参照)。右シフトする際、符号は保持されます。
> (parseInt('11111111111111111111111111111110', 2) >> 1).toString(2) '-1'−2を右シフトしました。結果は−1であり、すべての桁が1の32ビット整数(1の2の補数)に相当します。言い換えれば、1桁の符号付き右シフトは、負の数と正の数の両方を2で割ります。
number >>> digitCount(符号なし右シフト)> (parseInt('11100', 2) >>> 1).toString(2) '1110'ご覧のとおり、この演算子は左から0をシフトインします。
Number関数
Number関数は2つの方法で呼び出すことができます。
-
Number(value) 通常の関数として、
valueをプリミティブな数値に変換します(数値への変換を参照)。> Number('123') 123 > typeof Number(3) // no change 'number'-
new Number(num) コンストラクタとして、
Numberの新しいインスタンス(numをラップするオブジェクト)を作成します(プリミティブのラッパーオブジェクトを参照)。例えば> typeof new Number(3) 'object'
前者の呼び出し方が一般的です。
Numberコンストラクタのプロパティ
オブジェクトNumberには、以下のプロパティがあります。
-
Number.MAX_VALUE 表現可能な最大の正の数です。内部的には、小数部のすべての桁が1で、指数部は最大値の1023です。2を掛けて指数部を増やそうとすると、結果はエラー値
Infinityになります(Infinityを参照)。> Number.MAX_VALUE 1.7976931348623157e+308 > Number.MAX_VALUE * 2 Infinity
-
Number.MIN_VALUE 表現可能な最小の正の数です(0より大きく、非常に小さな分数):
> Number.MIN_VALUE 5e-324
-
Number.NaN - グローバルな
NaNと同じ値です。 -
Number.NEGATIVE_INFINITY > Number.NEGATIVE_INFINITY === -Infinity true
-
Number.POSITIVE_INFINITY > Number.POSITIVE_INFINITY === Infinity true
Numberプロトタイプメソッド
プリミティブ数値のすべてのメソッドはNumber.prototypeに格納されています(プリミティブはラッパーからメソッドを借用するを参照)。
Number.prototype.toFixed(fractionDigits?)
Number.prototype.toFixed(fractionDigits?)はfractionDigits桁に丸められた、指数を含まない数値の表現を返します。パラメータが省略された場合は、値0が使用されます。
> 0.0000003.toFixed(10) '0.0000003000' > 0.0000003.toString() '3e-7'
数値が1021以上の場合、このメソッドはtoString()と同じように機能します。指数表記の数値が得られます。
> 1234567890123456789012..toFixed() '1.2345678901234568e+21' > 1234567890123456789012..toString() '1.2345678901234568e+21'
Number.prototype.toPrecision(precision?)
Number.prototype.toPrecision(precision?)はtoString()と同様の変換アルゴリズムを使用する前に、仮数部をprecision桁に切り捨てます。精度が指定されていない場合は、toString()が直接使用されます。
> 1234..toPrecision(3) '1.23e+3' > 1234..toPrecision(4) '1234' > 1234..toPrecision(5) '1234.0' > 1.234.toPrecision(3) '1.23'
1234を3桁の精度で表示するには、指数表記が必要です。
Number.prototype.toString(radix?)
Number.prototype.toString(radix?)では、パラメータradixは、数値を表示する際の基数を示します。最も一般的な基数は、10(10進数)、2(2進数)、および16(16進数)です。
> 15..toString(2) '1111' > 65535..toString(16) 'ffff'
基数は少なくとも2以上、最大36以下でなければなりません。10より大きい基数では、アルファベット文字が桁として使用されるため、最大値が36になります。ラテンアルファベットには26文字があるためです。
> 1234567890..toString(36) 'kf12oi'
グローバル関数parseInt(parseInt()による整数を参照)を使用すると、そのような表記を数値に戻すことができます。
> parseInt('kf12oi', 36)
123456789010進数の指数表記
基数10の場合、toString()は、2つの場合に指数表記(小数点の前に1桁)を使用します。まず、数値の小数点の前に21桁以上ある場合。
> 1234567890123456789012 1.2345678901234568e+21 > 123456789012345678901 123456789012345680000
次に、数値が0.で始まり、その後に5つ以上の0と0以外の数字が続く場合。
> 0.0000003 3e-7 > 0.000003 0.000003
その他の場合、固定小数点表記が使用されます。
Number.prototype.toExponential(fractionDigits?)
Number.prototype.toExponential(fractionDigits?)は数値を指数表記で表現するように強制します。fractionDigitsは0から20までの数値で、小数点以下に表示する桁数を決定します。省略された場合は、数値を一意に指定するために必要なだけの有効桁数が含まれます。
この例では、toString()も指数表記を使用する場合に、より高い精度を強制しています。2進数を10進表記に変換する際の精度の限界に達するため、結果は混合しています。
> 1234567890123456789012..toString() '1.2345678901234568e+21' > 1234567890123456789012..toExponential(20) '1.23456789012345677414e+21'
この例では、数値の大きさはtoString()で指数が表示されるほど大きくありません。しかし、toExponential()は指数を表示します。
> 1234..toString() '1234' > 1234..toExponential(5) '1.23400e+3' > 1234..toExponential() '1.234e+3'
この例では、分数部分が小さすぎない場合に指数表記が得られます。
> 0.003.toString() '0.003' > 0.003.toExponential(4) '3.0000e-3' > 0.003.toExponential() '3e-3'
数値に関する関数
以下の関数は数値を操作します。
-
isFinite(number) numberが実際の数値であるかどうか(InfinityでもNaNでもない)をチェックします。詳細は、Infinityのチェックを参照してください。-
isNaN(number) numberがNaNの場合、trueを返します。詳細は、落とし穴:値がNaNかどうかをチェックするを参照してください。-
parseFloat(str) strを浮動小数点数に変換します。詳細は、parseFloat()を参照してください。-
parseInt(str, radix?) radix(2~36) を基数とする整数としてstrを解析します。詳細は、 parseInt() を使用した整数 を参照してください。
本章の参考文献
本章の執筆にあたり、以下の文献を参照しました。
[14] 出典: Brendan Eich, http://bit.ly/1lKzQeC.
[15] Béla Varga (@netzzwerg) は、IEEE 754 が NaN をそれ自身と等しくないものとして規定していることを指摘しました。